Cos'è un algoritmo?

Informalmente, un algoritmo è una procedura di calcolo ben definita, che prende uno o più valori come input e, da questi, restituisce uno o più valori come output.

Un algoritmo può essere considerato come uno strumento per risolovere un problema computazionale ben definito.

Quindi un algoritmo può essere considerato come una sequenza finita di passi che permette di risolvere un determinato problema.
schema algoritmo

Lo pseudocodice

Lo pseudocodice è un "liguaggio intermedio" tra la lingua parlata e il linguaggio di programmazione vero e proprio, ed è utilizzato per scrivere-progettare-modificare gli algoritmi prima di scriverlo in un linguaggio di programmazione vero e proprio.

Perché si utilizza?


Perché non è legato a nessun vincolo riguardante il linguaggio di programmazione da utilizzare e l'hardware (componenti fisiche conmpongono il computer).

A seguire gli pseudocodici degli algoritmi si troveranno nella parte di destra.

Breath First Search

La breath first search(bfs) o visita in ampiezza è un algoritmo di ricerca, che calcola la distanza da un punto di partenza S a un punto di arrivo D, gli input.

L'algoritmo sfrutta i colori per capire se una cella/posizione non è stata mai vista dall'algoritmo(white), se è tra le prossime ad essere visitate/attraversate (grey) o se è già stata attraversata (black).
Dopo che ha visitato una cella "mette in coda" (grey) le vicine di quest'ultima, prosegue così finché o non trova un cammino dal punto S al punto D o ci sono delle celle visitabili.
Al termine se è presente un cammino o percorso dal punto S a punto D, questo verrà restituito come output.

Questo algoritmo garantisce(se presente) uno dei possibili cammini minimi.

procedure BFS(G, s, d):

     for each vertex u ∈ G.V - {s} do:
         u.color = WHITE
         u.d = ∞
         u.π = NIL
     s.color = GREY
     s.d = 0
     s.π = NIL
     Q = Queue = {}
     enqueue(Q, s)
     while Q ≠ {} do:
         u = dequeue(Q)
         if s == d then:
             break
         for each v ∈ G.Adj[u] do:
             if v.color == WHITE then:
                 u.color = GREY
                 u.d = u.d + 1
                 u.π = u
                 enqueue(Q, v)
         u.color = BLACK
     PRINT-PATH(G, s, d)

end procedure

Deep First Search

La deep first search(dfs) o visita in profondità è un algoritmo di ricerca, che calcola la distanza da un punto di partenza S a un punto di arrivo D, gli input.

L'algoritmo sfrutta i colori per capire se una cella/posizione non è stata mai vista dall'algoritmo(white), se è tra le prossime ad essere visitate/attraversate (grey) o se è già stata attraversata (black) ed è "diviso" in 2 "parti".

Dopo che ha visitato una cella la "mette in coda" e passa alle sue successive (che non sono mai state viste), quando dopo una cella non ha più nulla in seguito, l'algortimo si muove a ritroso nelle celle che aveva lasciato in attesa (grey).
Al termine se è presente un cammino o percorso dal punto S a punto D, questo verrà restituito come output.

Questo algoritmo non garantisce(se presente) un cammino minimo.

procedure DFS(G, s, d):

     for each vertex u ∈ G.V - {s} do:
         u.color = WHITE
         u.π = NIL
     time = 0
     for each vertex u ∈ G.V - {s} do:
         if u.color == WHITE then:
             DFS-VISIT(G, u)

     PRINT-PATH(G, s, d)

end procedure

procedure DFS-VISIT(G, u):

     time = time + 1
     u.d = time
     u.color = GREY
     for each v ∈ G.Adj[u] do:
         if v.color == WHITE then:
             v.π = u
             DFS-VISIT(G, v)
     u.color = BLACK
     time = time + 1
     u.f = time

end procedure

Print Path

L'algoritmo printh path, si occupa di restituire la sequenza ordinata di celle/posizione ottenute da un algoritmo di ricerca.

procedure PRINT-PATH(G, s, d):

     if d == s then:
         print s
     else if v.π == NIL then:
         print "non ci sono cammini da 's' a 'd'"
     else:
         PRINT-PATH(G, s, d.π)
         print v

end procedure

A*

L'algoritmo A* (A star) è un algoritmo di ricerca da in punto S a un punto D, che garantisce un percorso minimo come la bfs, però è più complesso perché sfrutta delle "stime euristiche" per calcolare la mossa migliore da fare.

Questo è un esempio di ricerca best-first, cioè una strategia di ricerca informata.

Essendo di tipo "best-first", l'algoritmo tenderà ad esplorare le celle/posizioni più vicine alla destinazione.

Questo algoritmo garantisce(se presente) uno dei possibili cammini minimi.

procedure A*(G, s, d)

     for each vertex u ∈ G.V do:
         u.g_score = + ∞
         u.f_score = + ∞
         u.π = NIL
     s.g_score = 0
     s.f_score = Euclidean-Distance(s, d)
     open_list = PriorityQueue = {}
     closed_list = List
     open_list.enqueue(s, s.f_score)

     while open_list ≠ {} do:
         current = open_list.dequeue_less_priority()
         if current == d then:
             return PRINT-PATH(G, s, d)
         closed_list.push(current)

         for each neighbor ∈ G.Adj[u] do:
             tentative_score = current.g_score + Euclidean-Distance(current, neighbor)
             if tentative_score < neighbor.g_score:
                 neighbor.π = current
                 neighbor.g_score = tentative_score
                 neighbor.f_score = tentative_score + Euclidean-Distance(neighbor, d)

                 if neighbor not in open_list and neighbor not in closed_list:
                     open_list.enqueue(neighbor, neighbor.f_score)

     return "No path found"

end procedure

Faster A*

L'algoritmo faster A* (A star più veloce) è un algoritmo di ricerca da in punto S a un punto D.

Ha una struttura molto simile all'algoritmo A*, ma a differenza di quest'ultimo non tiene in considerazione la distanza con la posizione di partenza.

Questo algoritmo non garantisce(se presente) un cammino minimo.

procedure Faster-A*(G, s, d)

     for each vertex u ∈ G.V do:
         u.g_score = + ∞
         u.f_score = + ∞
         u.π = NIL
     s.g_score = 0
     s.f_score = Euclidean-Distance(s, d)
     open_list = PriorityQueue = {}
     closed_list = List
     open_list.enqueue(s, s.f_score)

     while open_list ≠ {} do:
         current = open_list.dequeue_less_priority()
         if current == d then:
             return PRINT-PATH(G, s, d)
         closed_list.push(current)

         for each neighbor ∈ G.Adj[u] do:
             tentative_score = current.g_score + Euclidean-Distance(current, neighbor)
             if tentative_score < neighbor.g_score:
                 neighbor.π = current
                 neighbor.g_score = tentative_score
                 neighbor.f_score = tentative_score + Euclidean-Distance(neighbor, d)

                 if neighbor not in open_list and neighbor not in closed_list:
                     open_list.enqueue(neighbor, Euclidean-Distance(neighbor, d))

     return "No path found"

end procedure

Euclidean Distance

Questo algoritmo è un algoritmo di "supporto", utilizzato per calcolare la distanza tra 2 punti, p1 e p2, nello spazio, a partire dalle loro coordinate cartesiane.

La distanza tra questi due punti è dato dalla radice quadrata della somma dei quadrati delle differenze tra le ordinate dei due punti
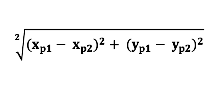
formula

procedure Euclidean-Distance(p1, p2)

     x_pow = pow(p2.x - p1.x, 2)
     y_pow = pow(p2.y - p1.y, 2)

     return sqrt(x_pow + y_pow)

end procedure